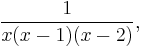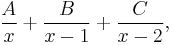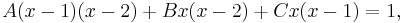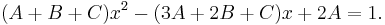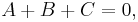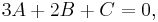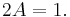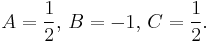Equating coefficients

In mathematics, the method of equating the coefficients is a way of solving a functional equation of two polynomials for a number of unknown parameters. It relies on the fact that two polynomials are identical precisely when all corresponding coefficients are equal. The method is used to bring formulas into a desired form.

Example

Suppose we want to apply partial fraction decomposition to the expression:

$\frac{1}{x(x-1)(x-2)},\,$

that is, we want to bring it into the form:

$\frac{A}{x}%2B\frac{B}{x-1}%2B\frac{C}{x-2},\,$

in which the unknown parameters are A, B and C. Multiplying these formulas by x(x − 1)(x − 2) turns both into polynomials, which we equate:

$A(x-1)(x-2) %2B Bx(x-2) %2B Cx(x-1) = 1,\,$

or, after expansion and collecting terms with equal powers of x:

$(A%2BB%2BC)x^2 - (3A%2B2B%2BC)x %2B 2A = 1.\,$

At this point it is essential to realize that the polynomial 1 is in fact equal to the polynomial 0x² + 0x + 1, having zero coefficients for the positive powers of x. Equating the corresponding coefficients now results in this system of linear equations:

$A%2BB%2BC = 0,\,$

$3A%2B2B%2BC = 0,\,$

$2A = 1.\,$

Solving it results in:

$A = \frac{1}{2},\, B = -1,\, C = \frac{1}{2}.\,$